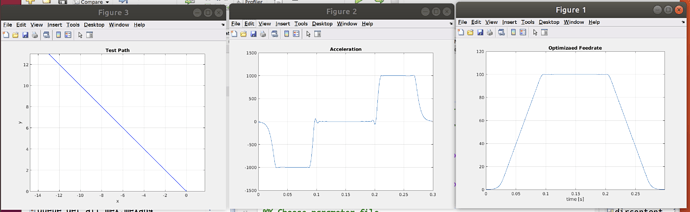
I did a simple test with the ngc file only contains one line segment.
Then I plot the pos/vel/acc profile.
It was found that the acceleration profile at the start and end of the curve is not a perfect line but a spline segment, which will influence the time optimality. But in the middle of the curve, the acceleration profile is almost a line segment. Does it have something to do with the Zero Speed problem? And is there any method to handle with it?
Yes, it has to do with the zero speed problem.
Clearly, for a straight line segment, the time-optimal acceleration profile must be a trapezoidal shape.
Your plot shows that this is almost the case, except at the beginning and at the end.
It seems to me that the starting phase with a constant pseudo jerk is not long enough.
When “switching” to the standard feedrate planning procedure too early, the q* approximation in the jerk constraint formulation gives a big conservatism, i.e. a loss of time.
Normally, in a machining zero speed situations are quite rare, and it’s not a tragedy if a little bit of time optimalitiy is lost.
But I will keep your point in mind; I believe that the “zero speed problem” could (and should) be better handled.
Thanks Raoul~
The loss of time optimality in CNC application may not be a problem because usually the tool path is very long. The duration at start and end phase could be neglected compared to the whole motion time.
But for a point to point move in robotic application, this start and end phase may occupy more percentage of the motion time. For instance, it may affect the pick and place cycle time ![]()
I agree for 100%.
I’m working on a profile generator (including jerk control) for pick and place operations.
It has nothing to do with the “feedopt” component of OpenCN.
This new profile generator will be a new component in OpenCN, especially for robotic pick and place operations.
It will also allow “following” an object on the conveyor at a certain non-zero speed before picking it.
Work in progress; if you are interested in, please take a look at the attached document.
PG_math.pdf (158.5 KB)
That’s cool!
Thanks for your sharing. I will take a look.