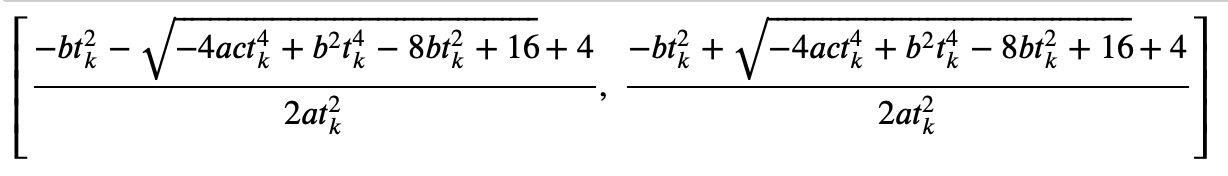Hi Raoul,
In the HPC paper, the remaining time is approximated by the following equation:
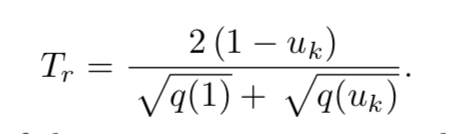
I’m wondering if this strategy could also be used for singularity handling. At the start of zero velocity, we can assume the q(u) to be linear, so we have the relation:
Then we have:
As q(uk) is a cubic spline and because q(0) is zero at start, we have q(u) to be the following format:
Substitute it into the denominator, we have:
This uk has a closed form of solution to be:
And we can choose the minimum positive solution.
We can use very small tk like 1e-8 to solve the uk, and the spline q(u) will be almost linear at the infinite-small range . Once we have the first solution, then we are safe to use Taylor series expansion to get the remaining uk.
Do you think the derivation is correct or did I mistake something?
Thanks!